Efekt Coandy – opis i analiza powstawania zjawiska

Cieknięcie po brodzie czy „ciągnięcie” po nogach raczej nie należy do najprzyjemniejszych zjawisk fizycznych. Wydawałoby się że jakaś niewidzialna siła przyciąga płyn akurat w to miejsce , które jest dla nas niekorzystne. Nie łączymy ze sobą jednak tych zjawisk ze sobą mimo to, że stoi za nimi ta sama przyczyna - jest efekt Coandy.
 

Cieknięcie po brodzie czy „ciągnięcie” po nogach raczej nie należy do najprzyjemniejszych zjawisk fizycznych. Wydawałoby się, że jakaś niewidzialna siła przyciąga płyn akurat w to miejsce, które jest dla nas niekorzystne. Nie łączymy ze sobą jednak tych zjawisk ze sobą mimo to, że stoi za nimi ta sama przyczyna tzw. efekt Coandy.

Efekt Coandy mówi nam o tym, że płyn ma tendencje do przylegania do najbliższej powierzchni. Definicja ta w dość dobry sposób obrazuje co się dzieje, natomiast kompletnie nie tłumaczy dlaczego do danego zjawiska zachodzi. Aby lepiej zrozumieć czym jest Efekt Coandy, jak go opisać oraz zrozumieć jakie niesie ze sobą konsekwencje postaram się go opisać na podstawie trzech przykładów.

Powierzchnia swobodna

Efekt Coandy najłatwiej zauważyć podczas przepływu cieczy w obecności powietrza, wynika to z widoczności płynu, gdzie gołym okiem widać poruszającą się ciecz w innym medium. Zbudowałem zatem stosunkowo proste badanie w celu wykazania tego efektu oraz przyjrzenia się mu bliżej. Badanie jest niestacjonarne, z uwzględnieniem działania sił masowych w postaci grawitacji a badanymi mediami tj. powietrzem i wodą, wypływającą ze źródła znajdującego się nad obiektem. Czas symulacji wynosił 1s, jest on wystarczający do powstania zamierzonego efektu.

Rys 1. Schemat badania

Zgodnie z logiką, struga po zmniejszeniu swojej grubości powinna przepłynąć obok obiektu, nie wchodząc z nim w interakcje. Zobaczmy zatem co jest wynikiem powyższej symulacji.

Rys 2. Wynik symulacji w postaci animacji przedstawiającej zachowanie strugi oraz ciśnienie względne powstające w wyniku działania przepływu.

Możemy zauważyć, że po jakimś czasie, struga wody, zaczęła przyklejać się do powierzchni, a następnie po jakimś czasie i przebyciu całej krzywizny odrywa się od obiektu. Zjawisko to musi powodować jakaś siła, która powoduje przyciągnięcie strugi i uniemożliwia jej przedwczesne oderwanie. Ta siła związana jest z podciśnieniem, które generuje się przy styku powierzchni z obiektem. W efekcie przepływu powstaje siła w kierunku X, która przyciąga strugę ku obiektowi. Patrząc jednak na symulacje powstaje zasadnicze pytanie, czy przyklejona struga generuje podciśnienie a za powstanie zjawiska odpowiada inna siła czy podciśnienie powoduje zmianę kierunku strugi, a potem utrzymuje je przy ścianie? Ze względu na wysoką gęstość wody i przez to stosunków wysokie wartości podciśnienia zmieniające się dość dynamicznie spróbujemy na to pytanie odpowiedzieć w dalszej części artykułu.

Analiza powstawania zjawiska

Aby wyjaśnić powstawanie tego zjawiska przeanalizujemy jeden z najbardziej powszechnych przykładów, przepływu nad podestem, bardzo często występujący w przypadku kalibracji modeli turbulencji. Dla naszego zagadnienia jednak wykorzystamy go w inny sposób.

Rys 3. Przedstawienie badanego modelu

Zgodnie z badaniem wykonanym na początku tego artykułu, struga wychodząca z półki powinna po jakimś czasie przylgnąć do podłoża. Symulacja ta pozwoli nam pokazać, czy wcześniej uzyskamy podciśnienie pod podestem czy jednak struga wcześniej dotknie podłoża. Wyniki powyższej symulacji przedstawione są na poniższej animacji.

Rys 4. Symulacja rozkładu prędkości oraz ciśnienia względnego.

Jednym z kluczowych momentów jest sytuacja dziejąca się około 0.335 sekundy. Widzimy że struga zaczyna zmierzać do podłoża[rys 5], natomiast pole ciśnienia względnego ma wartość ujemną w okolicy podestu[rys. 6], co powoduje zmianę kierunku strugi. A więc pole ciśnienia, powoduje zmianę kierunku strumienia, który powoduje dalsze zmniejszenia ciśnienia..

Rys 5. Przedstawienie pola prędkości w 0.335 s.

Rys 6. Przedstawienie częściowe pola ciśnienia względnego w 0.335 s.

Wynika to ze stosunkowo prostej zależności, struga przepływająca przez otoczenie, zabiera ze sobą cząstki z otoczenia. W miejsce tych cząstek zaczynają napływać nowe z otoczenia, w przypadku gdy uniemożliwimy taką sytuację, tworzy nam się zawirowanie, w którym jest mniej cząstek, a wiec i otrzymamy ujemną wartość ciśnienia względnego w efekcie czego, struga zaczyna się odchylać w kierunku ściany. Taka sama zależność ma miejsce w przypadku wykonanym z powierzchnią swobodną.

Rys 7. Przedstawienie trajektorii przepływu, ukazująca zasysanie cząstek przez strugę z otoczenia.

Dla tego przypadku pozostało nam odpowiedź na jeszcze dwa pytania, które mogłyby się nasunąć, czy rozmiar zawirowania przy podeście zależy od prędkości oraz ile procent strumienia wylotowego stanowi płyn, który nie wypływa z warunku brzegowego prędkości wlotowej. W tym celu przeprowadzono analizę parametryczną, gdzie zbadano pole prędkości w zależności od prędkości wlotowej warunku brzegowego. Zbadano prędkości od 1 m/s do 15 m/s z krokiem co 1 m/s.

Na rysunku 8 przedstawiono animacje, pokazująca zmianę pola prędkości , widzimy że zmieniają się praktycznie tylko i wyłącznie maksymalna wartość, natomiast sam kształt pola wygląda niemal identycznie.

Rys 8. Przedstawienie zmieniania pola prędkości w zależności od prędkości wlotowej

Dodatkowo zbadano wartość prędkości w kierunku X w odległości 2 mm od podłoża w celu sprawdzenia, w którym miejscu kończy się zawirowanie, przedstawiono je na rysunku 9, co potwierdza że punkt ten jest wspólny dla wszystkich prędkości, zatem efekt ten dla tego klasycznego warunku jest uzależniony stricte od geometrii.

Rys 9. Wykres pokazujący prędkość w kierunku X w zależności od prędkości wlotowej w odległości 2mm od podłoża.

Na rysunku 10 widzimy wykres względnej wielkości przepływu z otoczenia względem całkowitego strumienia.

Definicja tej wartości przedstawia się następująco:

Rys 10. Wykres względnego strumienia objętościowego w funkcji prędkości.

Widzimy zatem że dla tego modelu stanowi on około 35 %, niezależnie od warunków. Z tego powodu właśnie, dmuchając podczas rozpalania ogniska, robimy to z pewnej odległości, więcej tlenu dostaje się do paleniska.

Wykorzystanie praktyczne

Najczęściej ten efekt wykorzystywany jest w lotnictwie, gdzie dzięki zakończeniu skrzydła odpowiednim kształtem, jesteśmy w wstanie uzyskać dodatkową siłę nośną, takie przykładowe płaty możemy znaleźć na rysunku 11. Wykrzywienie na końcu sprawia, że struga po oderwaniu od płata, kieruje się w pożądanym kierunku. Efekt ten wykorzystują również wszelakiej maści lotki znajdujące się na skrzydłach co umożliwia sterowanie poprzez płaty.

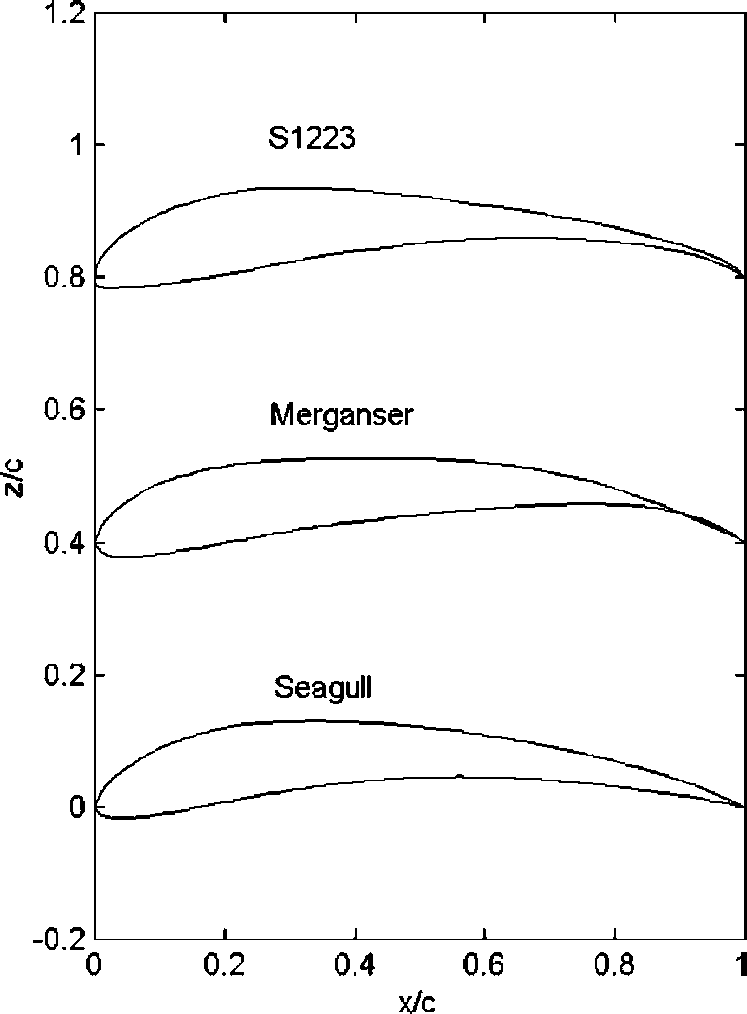
Rys. 11 Przykład profili lotniczych wykorzystujących efekt Coandy.

My natomiast skupimy się na mniej oczywistym wykorzystaniu tego zjawiska, wykażemy że pomocą odpowiedniego kształtu, możemy uzyskać siłę ciągu z wirnika promieniowego, jeżeli położymy go na półkolu. Przedstawienie schematu obliczeniowego możemy znaleźć na rysunku 12.

Rys. 12 Przedstawienie schematu badania.

Zgodnie z założeniami i tym co zostało pokazane wyżej, struga wychodząca z wentylatora, powinna przylgnąć do kształtu na którym leży i finalnie powinna być skierowana ku dołowi. W efekcie powinniśmy uzyskać siłę nośną dla całego układu. Wyniki analizy pokazano na rysunku 13, za pomocą trajektorii przepływu gdzie nasze przypuszczenia się potwierdziły.

Rys. 13 Wyniki analizy przedstawione za pomocą trajektorii przepływu wraz z wartością uzyskanej siły.

Drony tego rodzaju nie są nowością na rynku i są budowane od lat, np. jak ten ukazany na poniższym filmie.

Podsumowanie

Efekt Coandy, mimo tego, że nie jest zbyt znany, towarzyszy nam praktycznie wszędzie, zarówno w codziennym życiu jak i przy projektowaniu skomplikowanych urządzeń. Jednak świadome podejście do zagadnienia, pozwala na tworzenie coraz lepszych produktów i mam nadzieje, że powyższy artykuł wraz z animacjami oraz rysunkami, wizualizacjami wykonanymi w SOLIDWORKS Flow Simulation przybliżył Państwu zagadnienie na tyle, że swobodnie zaczną Państwo wykorzystywać to zjawisko.

Autor:

Karol SUCHOŃ

Inż. wsparcia technicznego CAD / SIM

,